Sweller’s Cognitive Load Theory (CLT) may be the single most important thing for teachers to know, but it was not necessarily designed with teachers in mind. The product of lab-based randomised controlled trials, it is a theory from the specific academic discipline Cognitive Science. In recent years teachers have found it incredibly useful and many blogs and books have been written trying to explain it and how it can be utilised in front-line education.
In my experience, most will use Willingham’s graphic below in order to explain CLT:
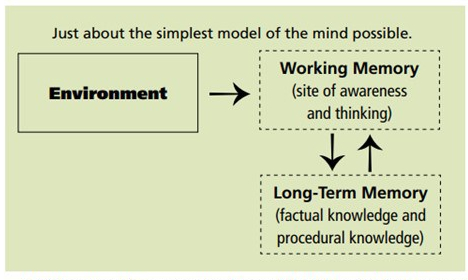
A very general reference to the working memory being limited will be made, and a discussion of how if it is “overloaded” learning cannot occur. To me, this is too general to be enormously useful (1). Often, blogs and articles can be more helpful by identifying specific aspects of CLT like dual coding or chunking, and though this is incredibly important, it doesn’t represent the full picture: it doesn’t give me enough to think about the load whatever the particular scenario.
In the technical literature, CLT is normally described by reference to extraneous, intrinsic and germane load. I have personally always found these terms to be a little cumbersome, and despite there being readable explanations out there like this, I’ve never particularly found the idea helpful.
A different presentation can be found in Frederick Reif’s book Applying Cognitive Science to Education. A physics educator by training, Reif has a very careful and analytic approach to tackling the issues that is often simplified into more readily understood presentations. His version of CLT reads as follows:
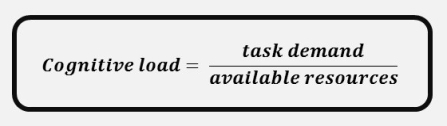
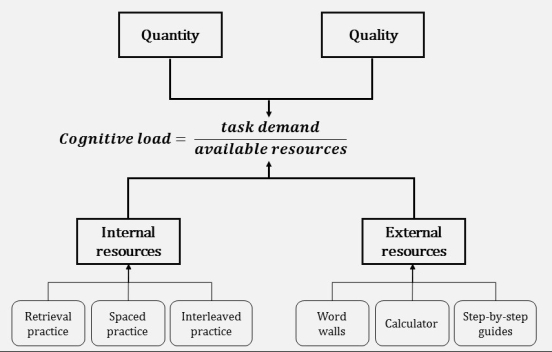
The science teacher in me really likes this. When presenting students with a formula like this, we would explain that increasing “task demand” increases load, whereas increasing “available resources” decreases load. Load, resources and demand are variables: they are things that can change, or be kept the same. This is important because there are some things that might be out of our control, and if that is the case we must manipulate the other variables to compensate. For example, the task demand of a GCSE paper is out of our hands, so we must therefore increase the resources available to the student to lower the overall load.
Before we look at the different parts of the equation, it is important to note that Reif is very clear that we should not be aiming to just lower the load as much as possible. He argues that if we do this the learning will take an incredibly long time as we make tasks smaller and smaller but also, importantly, that it will become exceedingly boring and demotivating for the student.
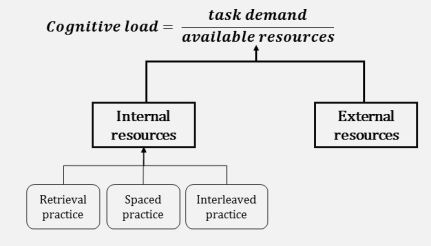
Let’s drill down into available resources first. This part of the equation can be thought of as the sum of two new variables:

Internal resources refers to the knowledge bank which a student has to bring to a particular task. This is where chunking and prior knowledge comes in: the more knowledge a student has of a particular domain, the easier it is for them to solve tasks relating to that domain. As teachers, we control this variable as much as possible through long-term memory strategies like retrieval practice, spacing practice and interleaving practice (2).
External resources refer to the physical objects from the environment that the student can use. In maths, this might be as simple as the use of a calculator or a piece of paper and a pen to do working on. In other subjects (including science) you might use a vocabulary wall which you can see demonstrated by Jo Facer here. In science specifically even the section on the periodic table where labels are shown pointing to “atomic number” and “mass number” will increase the external resources available to a student when they are working out the number of neutrons in a given atom. A step-by-step guide or list of rules for following a procedures would also probably count as external resources.
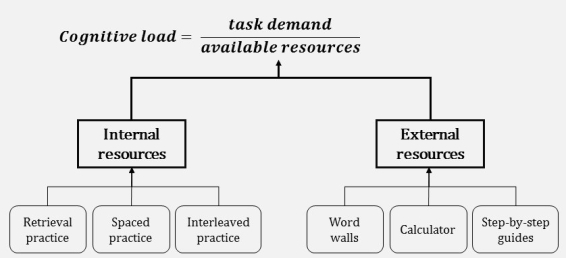
It might be interesting to consider attentional effects here as well. Though Reif does not discuss this, a quiet and orderly classroom is conducive to thinking and learning. If the classroom is noisy and distracted, then perhaps the external resources become lowered.
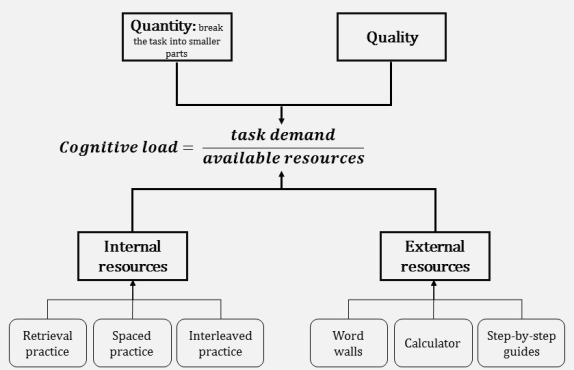
Task demand refers to the actual task which the student is completing. Reif discusses two ways of breaking down a task to lower its demand:
Quantity is the simplest to explain, as it just refers to the number of things in a particular task. So instead of asking students to derive and balance a particular symbol equation equation from a piece of text, you can break that down into 1) write a word equation 2) derive the formulae for each substance 3) construct a symbol equation 4) balance the symbol equation. In English for example, you might want students to be able to answer the question “How is Slim presented in this extract?” and break it down into 1) find a quotation that shows Slim being presented as empathetic, 2) analyse the methods the writer has used to show that he is empathetic, and so on for other characteristics (3).
I didn’t fully follow his explanation of quality, so in the interests of keeping this article simple, I’m not going to go into it. I don’t think as Reif describes it there are many useful applications in class (4).
Overall, we are therefore left with the below:
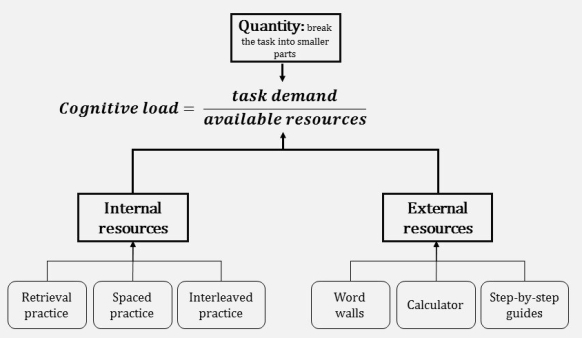
In my opinion, this mental model is a helpful framework for teachers to use when planning for learning. We can’t always control each of the variables, but by understanding that they relate to each other we can manipulate the ones we can control to result in an optimum load.
There is a follow-up post here which details how the model can be used to ensure that challenge is maintained throughout student practice and that support is correctly faded.
(1) I am of course aware that Willingham goes into more detail in his book and I highly recommend teachers read it. I am referring more to the “secondary” literature that has sprung up around it.
(2) For more reading on any of the concepts referred to throughout this blog, click here.
(3) Many thanks to Rebecca Foster for helping me out with this though I have probably misunderstood. English is not exactly my strong point…she has a brilliant blog about tackling complex tasks like writing an essay here.
(4) My understanding of quality runs as follows: it posits that there is some product you want to see from your students, which we will call P. If students are solving physics problems, P would be “interpret a text, extract the correct quantities, use and manipulate the correct formula, calculate answer, provide units.” A quantity model would just break all that up into smaller parts, so a bunch of questions on establishing correct quantities from texts, a bunch on manipulating formulae etc. A quality model says let us take an approximation of P, perhaps “describe how the quantities in a given text relate to each other.” This is a different type of task and gives students a series of approximations of P.
December 7, 2020 at 5:48 am
I’ve not read Reif, but if I were constructing the model myself then I would consider quality the precision/clarity of the task/problem. If the problem is clear cut, and it is obvious how it needs to be solved, then that informs what resources we need to draw on; however, if the problem is poorly defined, such that there is no immediately identifiable objective or solution, then we might need to draw on more resources in a sort of brute force or trial and error approach to solving, raising cognitive load.
Also, I wonder if a noisy classroom or otherwise distracting environment might not rather have the effect of increasing quantity rather than reducing resource? the more distractions there are, the more things one has to deal with while solving the problem, and one might even have to draw on additional resources to overcome the distractions.
These thoughts come only from reading this post and not from reading the primary literature.
LikeLiked by 2 people